Mélanges de corps purs, solutions et alliages
Définition
\(\triangleright\) Définition d'un solvant et des solutés
Dans un mélange, le solvant est le constituant le plus abondant.
Les autres constituants sont les solutés.
Mélanges à phase unique
Définition
\(\triangleright\) Définition des mélanges à phase unique
Dans un mélange à phase unique, on a \(k\) corps avec chacun une quantité de matière \(n_k\) dans une unique phase.
Potentiels chimiques
Potentiels thermodynamiquesPotentiel chimique
Mélange binaire
\(\triangleright\) Définition de la fraction molaire
La fraction molaire d'un mélange est définit comme:
$$x={{\frac{n_2}{n}} }$$
Avec:- \(n\): la quantité de matière du mélange
- \(n_2\): la quantité de matière du soluté
Enthalpie libre
\(\triangleright\) Définition d'une grandeur molaire partielle
On définit la grandeur molaire partielle \(z_i\) de chaque constituant dans le mélange par:
$$z_1={{\left(\frac{\partial Z}{\partial n_1}\right)_{T,P,n_2} }}$$
$$z_2={{\left(\frac{\partial Z}{\partial n_2}\right)_{T,P,n_1} }}$$
\(\triangleright\) Condition de stabilité chimique
Une des conditions locales de stabilité est donnée par la relation:
$${{\left(\frac{\partial \mu_i}{\partial n_i}\right)_{T,P,n_j\neq n_i}\gt 0}}$$
Mélanges séparé en plusieurs phases
Définitions
\(\triangleright\) Notations pour les mélanges
On définit les notations suivantes:- \(K\): le nombre de composantes
- \(\phi\): le nombre de phases
- \(n_i^{\alpha}\): le nombre de moles du constituant \(i\) dans la phase \(\alpha\)
- \(n^\alpha\): le nombre de moles dans la phase \(\alpha\)
Caractérisation
\(\triangleright\) Conditions d'équilibre entre les phase
Chaque phases se comporte comme un sous-système en contact non restrictif avec les autres phases.
Les conditions d'équilibre entre les phases sont:- égalité de température (échange thermique)
- égalité de pression (échange libre de volume)
- Egalité des potentiels chimiques (Potentiel chimique) pour chaque composant (échange de particules sans contrainte)
$$\mu_i^1=\mu_i^2=\mu_i^{\alpha}$$
\(\triangleright\) Caractérisation des phases
Pour caractériser les différentes phase, on fait appel aux variables suivantes:- \(P\) et \(T\), \(2\) variables intensives uniformes
- Les fractions molaires \(x^{\alpha}_i\), intensives au nombre de \((K-1)\)
- \(n^{\alpha}\) nombre de moles dans la phase \(\alpha\)
On a donc \(\phi(K-1)+2+\phi=\phi K+2\) variables intensives
Le nombre de variable intensive est donné par la Variance thermodynamique
Mélanges linéaires
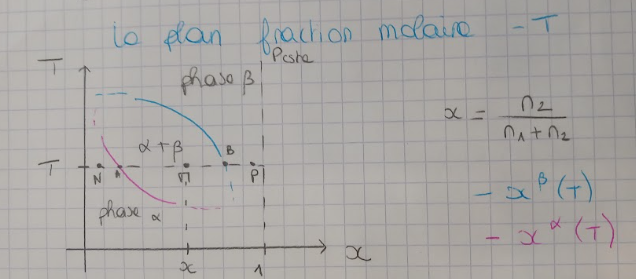
En présence de \(2\) phases, on aura:
$$x^{\alpha}(T,P)\quad et\quad x^{\beta}(T,P)$$
\(\triangleright\) Règles de lectures
Les règles de lectures sont les suivantes:- Si \({{x\lt x^{\alpha},x^{\beta} }}\), on sera en présence d'un mélange homogène
- Si \({{x\gt x^{\alpha}, x^{\beta} }}\), on sera en présence d'un mélange homogène
- Si \({{x^{\alpha}\lt x\lt x^{\beta}}}\), on sera en présence de coexistence de \(2\) phases
Cela vient des expressions suivantes qui se démontrent:
$$n^{\alpha}=\frac{x^{\beta} -x}{x^{\beta} -x^{\alpha} }(n_1+n_2)\gt 0$$
$$n^{\beta}=\frac{x -x^{\alpha}}{x^{\beta} -x^{\alpha} }(n_1+n_2)\gt 0$$
Théorème des moments (Mélange linéaire à 2 phases)
Diagrammes de phases
Diagrammes de phases
